Extent of Dissociation

Remember that in notes on Arrhenius Theory I briefly alluded to the fact that the percent dissociation for dilute acids was empirically found to depend on the initial concentration. Once we have the tools of equilibrium, we can actually see why that’s the case:

Consider an acid HA with some acidity constant Ka. Let’s take an initial solution with concentration $c_0$. The acid will dissociate:

$$\mathrm{HA}\rightleftharpoons \mathrm{H}{}^{+}+\mathrm{A}{}^{-}\text{\hspace{1em}(1)}$$

And let’s say the percent of an acid that will dissociate is $\alpha$. Meaning $[\mathrm{A}{}^{-}]=\alpha c_0$. By stoichiometry, this has to mean $[\mathrm{H}{}^{+}]=\alpha c_0$. Also, if you initially had $c_0$ of an acid, $\alpha c_0$ dissociated, then you have $c_0-\alpha c_0=(1-\alpha )c_0$ left, which is the concentration $[\mathrm{HA}]$. Let’s use the definition of $K_a$:

$$K_a=\frac{[\mathrm{H}{}^{+}][\mathrm{A}{}^{-}]}{[\mathrm{HA}]}=\frac{{\alpha }^2{c}_0^2}{(1-\alpha )c_0}\text{\hspace{1em}(2)}$$

From now on, we can take two different paths. We can either follow the historical path of reasoning or use the benefit of computer software and create some figures. Scroll down to the Ostwald Law of Dilution for the historical account, and I’m going to start with the modern day treatment first.

No Approximations

Let’s solve for $\alpha$ in (2):

$$\begin{array}{rl}{c}_0-\alpha c_0& =\frac{c_0^2}{K_a}{\alpha }^2\\ \frac{c_0^2}{K_a}{\alpha }^2+c_0\alpha -c_0& =0\\ c_0{\alpha }^2+K_a\alpha -K_a& =0\end{array}$$

Solving the quadratic equation:

$${\alpha }_{\pm }=\frac{-K_a\pm \sqrt{K_a^2+4K_a{c}_0}}{2c_0}$$

$\alpha$ has to be positive, so the only meaningful physical root is ${\alpha }_{+}$.

$$\alpha =\frac{-K_a+\sqrt{K_a^2+4K_a{c}_0}}{2c_0}\text{\hspace{1em}(3)}$$

First of all, it’d be nice to check our solution. We can easily do that using Python

from sympy import symbols, Eq, solve
 
alpha, Ka, c0 = symbols("alpha Ka c0")
equation = Eq(Ka, alpha**2 * c0**2 / ((1 - alpha) * c0))
solutions = solve(equation, alpha)

This gives us:

[(-Ka - sqrt(Ka*(Ka + 4*c0)))/(2*c0), (-Ka + sqrt(Ka*(Ka + 4*c0)))/(2*c0)]

Which is exactly what we found!

Ostwald Law of Dilution

We can manipulate (2) into:

$$\begin{array}{rl}{\alpha }^2{c}_0^2& =(1-\alpha )c_0{K}_a\\ \alpha c_0& =\sqrt{(1-\alpha )c_0{K}_a}\end{array}$$

For a dilute acid, it turns out that $\alpha$ is pretty small. Thus $1-\alpha \approx 1$. As a result:

$$\alpha c_0=[\mathrm{H}{}^{+}]=[\mathrm{A}{}^{-}]\approx \sqrt{c_0{K}_a}\text{\hspace{1em}(4)}$$

or:

$$\alpha =\frac{\sqrt{c_0{K}_a}}{c_0}=\sqrt{\frac{K_a}{c_0}}\text{\hspace{1em}(5)}$$

which is exactly the empirical relationship observed by Ostwald in 1890s.

If you wonder when $1-\alpha \approx 1$ is true, check out this page which dynamically plots $\alpha$ as a function of $c_0$ for different pKa values.

An amusing conjecture

You may wonder why do we bother talking about $\alpha$, it seems like a just another number, so what makes it worthy of so much attention? Remember that the initial formulation of Arrhenius theory didn’t employ the concepts of equilibrium. The most you could do is empirically calculate the fraction of acid that was dissociated $\alpha$ and observe that it inversely depended on concentration: $\alpha \propto 1/\sqrt{c_0}$. I think you agree that such relationship is quite troublesome: it says that the percent of an acid that dissociates is inversely related to the acid concentration. Dilute acids dissociate to a greater extent. It’s very counterintuitive that the fraction of acid that dissociates depends on the concentration in the first place, much more counterintuitive that the relationship is inverse.

Now can you imagine the relief when you learn that this is nothing but a mathematical artifact of the form of equilibrium constant $K_a$ (which stems from the equality in the reaction rates)? That there’s something constant after all? That this empiric dependence can actually be predicted with theory?

My conjecture is that all problems like Q1:

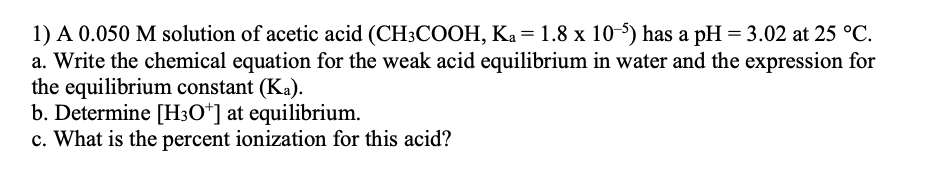
are structured in the way: 1) use Ka to calculate pH 2) find $\alpha$ as a demonstration of the superiority of the theory of equilibrium (or its validation) because it a) gives you new information b) perfectly agrees with what people already knew (which is $\alpha$ that people used to measure experimentally).

Which is actually a good indication of how science progresses. First you have a collection of experimental data points, from you which you can infer some correlations (such as $\alpha \propto 1/\sqrt{c_0}$), then someone makes a bold conjecture (such as the existence and establishment of equilibrium), develops a mathematical model which is first validated by explaining the currently known data and once you have that confidence in the model, you can start using its predictive power and calculate things you couldn’t find before.