Calculating Any pH

If I remember correctly, there were several interesting claims made in lecture:

strong acids dissociate fully, for weak acids we use a pKa value

and

in polyprotic weak acids, such as H3PO4, we can ignore the dissociation on every stage but the first one.

I actually see no benefit in all these shenanigans with making different rules for strong and weak acids and then having so many special cases. In reality, every acid, weak or strong, reacts with water in a reversible reaction:

HA + H X_{2} O A X^{-} + H X_{3} O X^{+} (1)

which can be characterized by an equilibrium constant or by $K_{a}$ . It’s just that if an acid has a very small pKa, such as $- 2$ , as you can verify here, the fraction of acid that reacts is essentially 1. Meaning that $[A X^{-}] = [H X_{3} O X^{+}] \approx c_{0}$ .

Can we ignore the second and third stages of H3PO4 dissociation? Yes, if we’re in a medium with $p H < 4$ . But not in general. As you can notice, the pseudo-rules above are nothing but special cases or just some observations which are true in certain conditions. In this note, I’ll show you that pH can be calculated without these pseudo-random assumptions.

Overview

We’ll proceed in several steps:

First, I’ll introduce a general framework for solving literally any problem that has to do with pH
I’ll show you that it leads to the same result for monoprotic acids as using the accounting table (or ICE table, if you prefer)
I’ll show you how it can be easily extended to diprotic acids (we’ll find exact pH of H2SO4)
I will show you another benefit of the general framework (the extension of ionization extent $α$ )
I’ll show you how with 4 you can easily tackle even triprotic acids (such as H3PO4)

1. The Framework for Solving Any Problem

Write the chemical equation for every process that occurs in your system.
Write the equilibrium constant for every process above
Write the equation for the mass balance constraint
Write the equation for the electroneutrality constraint

The first two are self-explanatory, let’s elaborate on 3rd and 4th step.

Mass Balance Constraint

Matter cannot spontaneously come into existence from the void nor can it similarly disappear. As a result, if we, say, initially had some acid $[HA] = c_{0}$ in exclusively protonated form, post deprotonation, the total amount of atoms composing $A$ is unchanged. Once we reach equilibrium, $A$ is stored in two forms: $HA$ and $A X^{-}$ . Mass balance constraint says that the sum of these concentrations must be equal to $c_{0}$ :

[HA] + [A X^{-}] = c_{0} (2)

Electroneutrality Constraint

The absolute majority of matter in its stable (read: commonly occurring form) is electrically neutral. This is a fundamental principle that you use to write molecular formula of different compounds. When you try to write the formula for iron oxide, $Fe X^{3 +} O X^{2 -}$ you argue that the molecule has to be neutral, so for every 2 atoms of iron, you must have 3 atoms of oxygen $Fe X_{2} O X_{3}$ . Similar electroneutrality can be applied to solutions: the sum total of negatively charged ions should be equal to the sum total of positively charged ions.

You could also think of electroneutrality as a “charge balance equation” (allusion to the mass balance above). This approach also helps to understand why we must multiply the concentration of an ion by the magnitude of its charge. For example, in a solution of $H X_{2} SO X_{4}$ , you can have the following ions: $H X_{3} O X^{+}, HSO X_{4} X^{-}, SO X_{4} X^{2 -}$ . Charge balance says:

[H X_{3} O X^{+}] = [HSO X_{4} X^{-}] + 2 [SO X_{4} X^{2 -}] (3)

This may seem a bit unintuitive at first, at least that was my experience, but think about it as counting total charge on the left and on the right. Every $SO X_{4} X^{2 -}$ brings two charges, so the total quantity of negative charge is double the concentration of $SO X_{4} X^{2 -}$ .

2. Monoprotic Acids

Let’s see how the framework above can be applied to monoprotic acids. First, we write the chemical equation for every equilibrium in the mixture. In this case, we only have proton transfer with water:

HA + H X_{2} O A X^{-} + H X_{3} O X^{+} (1)

As a result, in the solution you might have $HA, A X^{-}, H X_{3} O X^{+}$ .

Second, we write the equilibrium constant for that process:

K_{a} = \frac{[ A X ^{-} ] [ H X _{3} O X ^{+} ]}{[ HA ]} (4)

Third, we write material balance:

[HA] + [A X^{-}] = c_{0} (2)

and electric neutrality:

[A X^{-}] = [H X_{3} O X^{+}] (5)

We presume $K_{a}$ and $c_{0}$ is known. Then, we have 3 equations (2, 4, 5) and 3 unknowns: $[H X_{3} O X^{+}], [HA], [A X^{-}]$ . The solution then exists and is unique. We can substitute (5) into (2):

[HA] + [H X_{3} O X^{+}] = c_{0} ⟹ [HA] = c_{0} - [H X_{3} O X^{+}] (6)

and then (6) into (4):

K_{a} = \frac{[ H X _{3} O X ^{+} ] ^{2}}{c _{0} - [ H X _{3} O X ^{+} ]} (7)

Resulting in an equation with just one unknown. Remarkably, this is identical to the result we obtained before using stoichiometric accounting approach. Let’s state, for completeness, that the solution to quadratic equation (7) is:

[H X_{3} O X^{+}] = \frac{- K _{a} + K _{a}^{2} + 4 K _{a} c _{0}}{2}

3. Diprotic Acids. H2SO4.

The beauty of the framework presented is that it can be easily extended to any acid. I can imagine you could write out the stoichiometry for polyprotic acids as well, but I think the calculation becomes significantly more difficult.

First, writing chemical equations of every process:

H X_{2} SO X_{4} + H X_{2} O HSO X_{4} X^{-} + H X_{2} O HSO X_{4} X^{-} + H X_{3} O X^{+} SO X_{4} X^{2 -} + H X_{3} O X^{+} (8) (9)

Then writing equilibrium constants:

K_{a 1} K_{a 2} = \frac{[ HSO X _{4} X ^{-} ] [ H X _{3} O X ^{+} ]}{[ H X _{2} SO X _{4} ]} = \frac{[ SO X _{4} X ^{2 -} ] [ H X _{3} O X ^{+} ]}{[ HSO X _{4} X ^{-} ]} (10) (11)

Mass balance:

c_{0} = [H X_{2} SO X_{4}] + [HSO X_{4} X^{-}] + [SO X_{4} X^{2 -}] (12)

And electroneutrality:

[H X_{3} O X^{+}] = [HSO X_{4} X^{-}] + 2 [SO X_{4} X^{2 -}] (13)

Analytical Solution

Now, let’s express $[H X_{2} SO X_{4}]$ from (10) and $[SO X_{4} X^{2 -}]$ from (11) and plug that into (12):

c_{0} c_{0} c_{0} [HSO X_{4} X^{-}] = \frac{[ HSO X _{4} X ^{-} ] [ H X _{3} O X ^{+} ]}{K _{a 1}} + [HSO X_{4} X^{-}] + \frac{K _{a 2} [ HSO X _{4} X ^{-} ]}{[ H X _{3} O X ^{+} ]} = [HSO X_{4} X^{-}] (\frac{[ H X _{3} O X ^{+} ]}{K _{a 1}} + 1 + \frac{K _{a 2}}{[ H X _{3} O X ^{+} ]}) = [HSO X_{4} X^{-}] (\frac{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}}{K _{a 1} [ H X _{3} O X ^{+} ]}) = \frac{K _{a 1} [ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} c_{0} (14)

You might see now that the choice of what to express and plug was done so that at the end we would be able to express $[HSO X_{4} X^{-}]$ as a function of $K_{a 1}, K_{a 2}, c_{0}$ which are known and $[H X_{3} O X^{+}]$ . You might see that if we were to succeed with repeating this for $[SO X_{4} X^{2 -}]$ , we could plug everything into (13) and have one equation with one unknown: $[H X_{3} O X^{+}]$ . This is the plan.

Let’s multiply both sides of (10) by (11):

K_{a 1} K_{a 2} = \frac{[ SO X _{4} X ^{2 -} ] [ H X _{3} O X ^{+} ] ^{2}}{[ H X _{2} SO X _{4} ]} (15)

Let’s express $[H X_{2} SO X_{4}]$ from (15) and $[HSO X_{4} X^{-}]$ from (11) and plug that into (12):

c_{0} c_{0} c_{0} [SO X_{4} X^{2 -}] = \frac{[ SO X _{4} X ^{2 -} ] [ H X _{3} O X ^{+} ] ^{2}}{K _{a 1} K _{a 2}} + \frac{[ SO X _{4} X ^{2 -} ] [ H X _{3} O X ^{+} ]}{K _{a 2}} + [SO X_{4} X^{2 -}] = [SO X_{4} X^{2 -}] (\frac{[ H X _{3} O X ^{+} ] ^{2}}{K _{a 1} K _{a 2}} + \frac{[ H X _{3} O X ^{+} ]}{K _{a 2}} + 1) = [SO X_{4} X^{2 -}] (\frac{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O ] + K _{a 1} K _{a 2}}{K _{a 1} K _{a 2}}) = \frac{K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O ] + K _{a 1} K _{a 2}} c_{0} (16)

Okay, now let’s take the result of (14) and (16) and plug that into (13):

[H X_{3} O X^{+}] [H X_{3} O X^{+}] = [HSO X_{4} X^{-}] + 2 [SO X_{4} X^{2 -}] = \frac{K _{a 1} [ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} c_{0} + \frac{2 K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O ] + K _{a 1} K _{a 2}} c_{0}

Which leads us to:

[H X_{3} O X^{+}]^{3} + K_{a 1} [H X_{3} O X^{+}]^{2} + K_{a 1} K_{a 2} [H X_{3} O X^{+}] = K_{a 1} [H X_{3} O X^{+}] c_{0} + 2 K_{a 1} K_{a 2} c_{0}

or:

[H X_{3} O X^{+}]^{3} + K_{a 1} [H X_{3} O X^{+}]^{2} + (K_{a 1} K_{a 2} - K_{a 1} c_{0}) [H X_{3} O X^{+}] - 2 K_{a 1} K_{a 2} c_{0} = 0 (17)

which is a cubic polynomial. Cubic polynomials are not as easy to solve as quadratic ones, but it’s actually still doable. See this primer if you’re curious how.

Is it worth it?

We need to make a few comments regarding derivation above. Looking at the derivation above, it’s tempting to think: maybe it’s worth having some arbitrary empirical rules on strong/weak acids if it allows to avoid doing the manipulations above. I actually think that doing derivations like above is the very reason why everyone should take a STEM course.

Let me explain. I’ve said this multiple times already, but learning science is not just limited to learning what is an acid or how to calculate a pH or an equilibrium constant. The ability to do that does determine your grade, yes, but what’s orders of magnitude more important is a) the thinking skills you develop in the process and b) the abstractions and lessons you take on how to approach problem-solving in general. The derivation above is a good way for those thinking skills to develop. Besides, there’s a very important lesson you learn in the process.

You might wonder: how could have I known that I should express $[H X_{2} SO X_{4}]$ from (10) and $[SO X_{4} X^{2 -}]$ from (11) and plug that into (12)? You couldn’t. A good exercise is to start from (10)-(13) and then, not looking at these notes, somehow derive (14). I think it’s impossible to achieve that by simply staring at the equations (10)-(13) and (14). You have to try and do something. Maybe first express $[H X_{3} O X^{+}]$ . Does it bring you closer to the desired result? No? Let’s do something different. Let’s try to express $HSO X_{4} X^{-}$ . Does it help? It’s an inherently iterative process which leads to dead ends most of the time. With time, you might start noticing certain patterns, which allow you to make certain shortcuts. With even more time, you might be able to start doing these shortcuts in your head. Which is really how I wrote the derivation above (I didn’t consult any notes in deriving it, fyi). The first time I’ve tried to derive (14) or (16), I think I spent at least 2 or 3 hours doing random substitutions ending in a trivial result (such as $K_{a 1} = K_{a 1}$ ) 99% of the time. You might wonder: is it a good way to spend 2 or 3 hours? Experiences like that, I think, are the primary reason why I have the confidence that I can tackle any problem I face. I just need to try different things and not expect to get it right from the first attempt. So if you think having that confidence is good, then it’s a very good way to spend 2 or 3 hours.

Yet Another Chance for Python to Shine

when we discussed bringing equations to linear form many moons ago, I argued that Python is one of the most useful tools you might add to your arsenal. Here’s another demonstration of that claim. Let’s verify (14) and (16) using Python:

from sympy import symbols, Eq, solve
Ka1, Ka2, Ka1Ka2, c0, H2SO4, HSO4_minus, SO4_2minus, H3O_plus = symbols(
"Ka1 Ka2 Ka1Ka2 c0 H2SO4 HSO4_minus SO4_2minus H3O_plus"
)
 
eq1 = Eq(Ka1, (HSO4_minus * H3O_plus) / H2SO4)
eq2 = Eq(Ka2, (SO4_2minus * H3O_plus) / HSO4_minus)
 
# Mass balance equation
eq3 = Eq(c0, H2SO4 + HSO4_minus + SO4_2minus)
# Electroneutrality equation
eq4 = Eq(H3O_plus, HSO4_minus + 2 * SO4_2minus)
 
solution = solve(
	(eq1, eq2, eq3), # specifying systems of equations to solve
	[H2SO4, HSO4_minus, SO4_2minus], # specifying variables that we want to express
	exclude=[Ka1, Ka2, c0, H3O_plus], # specifying variables that we can treat as known (the variables above will be expressed in terms of these)
	dict=True,
	)

The solution it finds is:

[{
  H2SO4: H3O_plus**2*c0/(H3O_plus**2 + H3O_plus*Ka1 + Ka1*Ka2), 
  HSO4_minus: H3O_plus*Ka1*c0/(H3O_plus**2 + H3O_plus*Ka1 + Ka1*Ka2), 
  SO4_2minus: Ka1*Ka2*c0/(H3O_plus**2 + H3O_plus*Ka1 + Ka1*Ka2)
  }]

Which is exactly (14) and (16)! Just fyi, raising a number to some power in Python is denoted by two asterisks **. That is 3**2 denotes $3^{2}$ . It also shows an expression of H2SO4 which we haven’t derived yet, but will do that in the next section.

We can substitute these into equation 4 and try to simplify:

from sympy import simplify
eq4_substituted = eq4.subs(
{HSO4_minus: solution[0][HSO4_minus], SO4_2minus: solution[0][SO4_2minus]}
)
simplified_eq4 = simplify(eq4_substituted)

Which gives us: 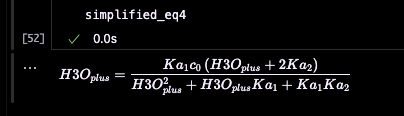Ugh, it doesn’t bring it to the polynomial form. If we want to enforce it, we could ask it to simplify the multiplication

polynomial_eq = simplify(
	simplified_eq4.lhs * (H3O_plus**2 + H3O_plus * Ka1 + Ka1 * Ka2)
	- simplified_eq4.rhs * (H3O_plus**2 + H3O_plus * Ka1 + Ka1 * Ka2)
)

Which gives us 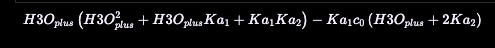which is (17) exactly. Since we’re here, we can ask it to find pH of 0.1 M $H X_{2} SO X_{4}$ for which pK $_{a 1} = - 2.8$ , and pK $_{a 2} = 1.99$ :

Ka1_val = 10 ** (2.8)
Ka2_val = 10 ** (-1.99)
c0_val = 0.1
polynomial_eq_values = polynomial_eq.subs({Ka1: Ka1_val, Ka2: Ka2_val, c0: c0_val})
 
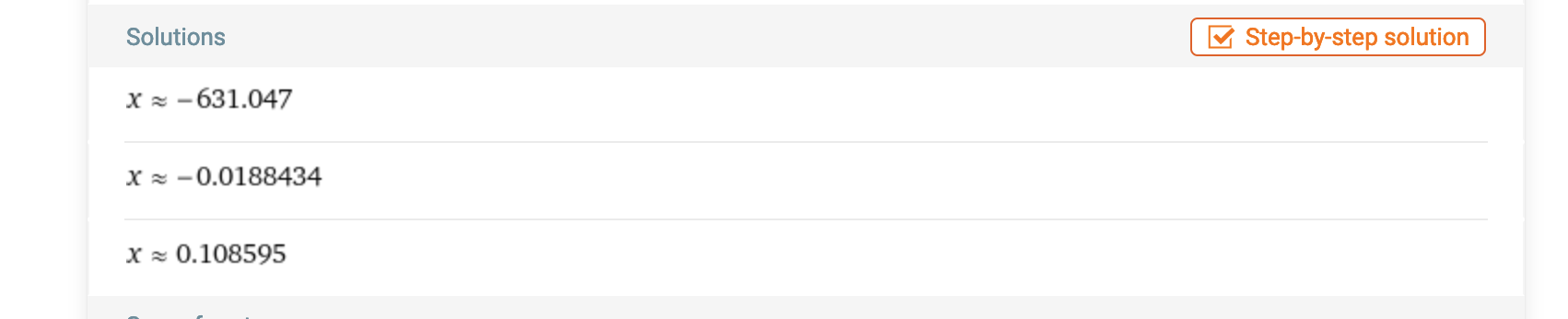
solutions_H3O_plus = solve(polynomial_eq_values, H3O_plus)

Which gives us:

[-631.047095540396 + 0.e-22*I, 
 -0.0188434475229529 + 0.e-23*I, 
 0.108594507725938 - 0.e-23*I]

The I stands for the imaginary $i$ (from complex numbers), but 0e-23 is 0, so all roots are real. If we take the negative log of it, we find that pH is equal to 0.9642. Which is essentially identical to the solution you obtain if you were to assume that dissociation occurs completely for the first stage.

You could also simply plug the values into (17) and feed it into WolframAlpha:

x^{3} + 1 0^{2.8} x^{2} + (1 0^{0.81} - 1 0^{2.8} * 0.1) x - 2 * 1 0^{0.81} * 0.1 = 0

Good!

4. Extending Extent of Dissociation

When we discussed Arrhenius theory, we often used a metric $α$ to show what fraction of an acid dissociates into $A X^{-}$ . This metric can be extended to polyprotic acids. Let’s define $α$ to be the fraction of the acid that exists in a given form:

α_{HA} = \frac{[ HA ]}{c _{0}} α_{A X^{-}} = \frac{[ A X ^{-} ]}{c _{0}} (18)

and similarly for a diprotic acid:

α_{H X_{2} A} = \frac{[ H X _{2} A ]}{c _{0}} α_{HA X^{-}} = \frac{[ HA X ^{-} ]}{c _{0}} α_{A X^{2 -}} = \frac{[ A X ^{2 -} ]}{c _{0}} (19)

If you look at (14) and (16), you might notice that we have everything we need to express two of these alphas!

α_{HSO X_{4} X^{-}} = \frac{[ HSO X _{4} X ^{-} ]}{c _{0}} = \frac{K _{a 1} [ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} (20)

and

α_{SO X_{4} X^{2 -}} = \frac{[ SO X _{4} X ^{2 -} ]}{c _{0}} = \frac{K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O ] + K _{a 1} K _{a 2}} (21)

Equations (20) and (21) allow us to determine the fraction of an acid that will be present in the form of $HA X^{-}$ and $A X^{2 -}$ at any given pH

For completeness, let’s try to express $α_{H X_{2} SO X_{4}}$ . To do that, we need to express $[HSO X_{4} X^{-}]$ from (10) and $[SO X_{4} X^{2 -}]$ from (14) and plug that into (12):

c_{0} c_{0} c_{0} α_{H X_{2} SO X_{4}} = [H X_{2} SO X_{4}] + \frac{K _{a 1} [ H X _{2} SO X _{4} ]}{[ H X _{3} O X ^{+} ]} + \frac{K _{a 1} K _{a 2} [ H X _{2} SO X _{4} ]}{[ H X _{3} O X ^{+} ] ^{2}} = [H X_{2} SO X_{4}] (1 + \frac{K _{a 1}}{[ H X _{3} O X ^{+} ]} + \frac{K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2}}) = [H X_{2} SO X_{4}] (\frac{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2}}) = \frac{[ H X _{2} SO X _{4} ]}{c _{0}} = \frac{[ H X _{3} O X ^{+} ] ^{2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} (22)

If you wonder how do these alphas look like at different pH and at different pKa values, check out this page

Expressing Alpha for Monoprotic Acid

Let’s try an express alphas in a similar manner for a monoprotic acid. Recall the expression for the equilibrium constant:

K_{a} = \frac{[ A X ^{-} ] [ H X _{3} O X ^{+} ]}{[ HA ]} (4)

and the equation of material balance:

[HA] + [A X^{-}] = c_{0} (2)

Let’s express $[HA]$ from (4) and plug into (2):

\frac{[ A X ^{-} ] [ H X _{3} O X ^{+} ]}{K _{a}} + [A X^{-}] [A X^{-}] (\frac{[ H X _{3} O X ^{+} ]}{K _{a}} + 1) [A X^{-}] (\frac{[ H X _{3} O X ^{+} ] + K _{a}}{K _{a}}) α_{A X^{-}} = c_{0} = c_{0} = c_{0} \equiv \frac{[ A X ^{-} ]}{c _{0}} = \frac{K _{a}}{[ H X _{3} O X ^{+} ] + K _{a}} (23)

if instead we express $[A$ from (4) and plug into (2):

[HA] + \frac{K _{a} [ HA ]}{[ H X _{3} O X ^{+} ]} [HA] (1 + \frac{K _{a}}{[ H X _{3} O X ^{+} ]}) [HA] (\frac{[ H X _{3} O X ^{+} ] + K _{a}}{[ H X _{3} O X ^{+} ]}) α_{HA} = c_{0} = c_{0} = c_{0} \equiv \frac{[ HA ]}{c _{0}} = \frac{[ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] + K _{a}} (24)

You may think that this alpha is different from the one we’ve seen before. After all, the formula we’ve obtained before was slightly different. Specifically, we had:

α_{A X^{-}} = \frac{- K _{a} + K _{a}^{2} + 4 K _{a} c _{0}}{2 c _{0}} (25)

You can get to equation (25) from (23) if you recall that in the case of a monoprotic acid $[H X_{3} O X^{+}] = [A X^{-}]$ (which happens to coincide with electroneutrality constraint, so $α_{A X^{-}} c_{0} = [H X_{3} O X^{+}]$ . As a result:

α_{A X^{-}} = \frac{K _{a}}{α _{A X^{-}} c _{0} + K _{a}}

You can see that this is an equation with one unknown, so you can solve it for $α_{A X^{-}}$ and get the expression (25).

5. Triprotic Acids

Let’s write out alphas for monoprotic and diprotic acids again:

α_{HA} = \frac{[ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] + K _{a}} α_{A X^{-}} = \frac{K _{a}}{[ H X _{3} O X ^{+} ] + K _{a}}

and

α_{H X_{2} A} α_{HA X^{-}} α_{A X^{2 -}} = \frac{[ H X _{3} O X ^{+} ] ^{2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} = \frac{K _{a 1} [ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}} = \frac{K _{a 1} K _{a 2}}{[ H X _{3} O X ^{+} ] ^{2} + K _{a 1} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2}}

Do you notice any patterns?

I’m going to tell you what I see. Let’s look at alphas for diprotic acid first. The denominator is the same for all forms, and the numerator has some combination of $[H X_{3} O X^{+}], K_{a 1}, K_{a 2}$ . The fully protonated form with two protons has $[H X_{3} O X^{+}]$ raised to the power of two. The form with one proton which forms in the first dissociation has one $[H X_{3} O X^{+}]$ and one $K_{a 1}$ . The form that results from two dissociations according to $K_{a 1}$ and $K_{a 2}$ has both of those in the numerator. So it appears as if the general rule is: start with fully protonated form and use $[H X_{3} O X^{+}]$ to the power of the number of hydrogens in that form. Then, to get an alpha for each successive form, remove one from the power of $[H X_{3} O X^{+}]$ and multiply by the $K_{a}$ of each stage.

Will you be surprised if I tell you that if you do all the steps: write expressions for $K_{a 1}, K_{a 2}, K_{a 3}$ for a triprotic acid, write the material balance constraint, do some manipulations, you’ll get:

α_{H X_{3} A} α_{H X_{2} A X^{-}} α_{HA X^{2 -}} α_{A X^{3 -}} = \frac{[ H X _{3} O X ^{+} ] ^{3}}{[ H X _{3} O X ^{+} ] ^{3} + K _{a 1} [ H X _{3} O X ^{+} ] ^{2} + K _{a 1} K _{a 2} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2} K _{a 3}} = \frac{K _{a 1} [ H X _{3} O X ^{+} ] ^{2}}{[ H X _{3} O X ^{+} ] ^{3} + K _{a 1} [ H X _{3} O X ^{+} ] ^{2} + K _{a 1} K _{a 2} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2} K _{a 3}} = \frac{K _{a 1} K _{a 2} [ H X _{3} O X ^{+} ]}{[ H X _{3} O X ^{+} ] ^{3} + K _{a 1} [ H X _{3} O X ^{+} ] ^{2} + K _{a 1} K _{a 2} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2} K _{a 3}} = \frac{K _{a 1} K _{a 2} K _{a 3}}{[ H X _{3} O X ^{+} ] ^{3} + K _{a 1} [ H X _{3} O X ^{+} ] ^{2} + K _{a 1} K _{a 2} [ H X _{3} O X ^{+} ] + K _{a 1} K _{a 2} K _{a 3}}

Nice, isn’t it? You could verify by doing the derivation or using sympy, if you want. If you’d like to find pH of the triprotic acid, you could write the electric neutrality:

[H X_{3} O X^{+}] = [H X_{2} A X^{-}] + 2 [HA X^{2 -}] + 3 [A X^{3 -}]

Because alphas depend only on the Ka’s, which are known, you can get concentrations of every form in the right hand side by multiplying by $c_{0}$ , which is also known. All you’ll have to do is to solve a polynomial of the 4th degree. Which is very impractical to do by hand, but a WolframAlpha or SymPy can do that for you quite happily!

Chem165 Notes

Explorer