Collision Theory

This time we perform a more rigorous treatment of the energetics of reactions.

The best part about doing theory is that you can construct models as if you’re playing with a constructor. We want to model the rate of chemical reaction $\mathrm{A}+\mathrm{B}\to \mathrm{C}$. Let’s call it $r$.

We’ve established that the rate of collisions is proportional to relative number of molecules. Thus, if the number of molecules per unit volume is $n_A=N_A/V$ in units of molecules per m^3 (we use meters because they’re standard units).

$$r\propto n_A{n}_B$$

In practice, we like to deal with concentrations in mols, so it’d be better if we could convert those relative numbers to mol/L.

$$\begin{array}{rl}{n}_A& =\frac{\text{molecule}}{m^3}\\ n_A\times \frac{1}{10^3}& =\frac{\text{molecule}}{m^3}\times \frac{1m^3}{10^{3}L}\\ n_A\times \frac{1}{N_A}\frac{1}{10^3}& =\frac{\text{molecule}}{m^3}\times \frac{1m^3}{10^{3}L}\times \frac{1mol}{N_A\text{ molecules}}\end{array}$$

Thus, $[A]=n_A/(N_A\times 10^3)$. Or, $n_A=10^3{N}_A[A]$. Therefore, our reaction rate becomes:

$$r\propto 10^6{N}_A^2[A][B]$$

Then we can recall saying that we could quantify the chance that two particles meet by looking at their sizes: bigger molecules have greater chance of meeting each other.

![[cross [email protected]]] A key mathematical insight is that molecule $A$ with radius $r_A$ collides with molecule $B$ with radius $r_B$ whenever the center of the molecule $A$ lies within the circle centered at the center of the molecule $B$ with radius $r_A+r_B$. Therefore, out of all possible positions for the center of molecule $A$, only $\pi (r_A+r_B{)}^2$ correspond to collisions. This value is often called a collision cross-section $\sigma$. The greater this value - the more likely a collision will happen, so:

$$r\propto \sigma 10^6{N}_A^2[A][B]$$

then we can recall that we can increase number of collisions if molecules move faster. Okay, so then we should consider an average speed of molecules, which equals to (a result derived from kinetic theory of gases):

$$v_{mean}=\sqrt{\frac{8RT}{\pi \mu }}$$

where $\mu$ is something called reduced mass:

$$\mu =\frac{m_A{m}_B}{m_A+m_B}$$

Long story short, the use of $\mu$ allows us to find the relative speeds of molecules, not just absolute ones. Okay, then:

$$r\propto \sigma \sqrt{\frac{8RT}{\pi \mu }}10^6{N}_A^2[A][B]$$

Finally, we can recall that only collisions, which have enough energy lead to chemical reactions. The fraction of molecules which has energy above $E_a$ is:

$$e^{-E_a/RT}$$

Finally, our reaction rate becomes:

$$r\propto \sigma \sqrt{\frac{8RT}{\pi \mu }}10^6{N}_A^2{e}^{-E_a/RT}[A][B]$$

But this $r$ counts number of collisions in absolute numbers. In practice, we’re interested in number of mols of collisions, so we should divide both sides by $N_A$:

$$r\propto \sigma \sqrt{\frac{8RT}{\pi \mu }}10^6{N}_A{e}^{-E_a/RT}[A][B]$$

Let’s do dimensions analysis. $\sigma$ has units of $m^2$. the thing in square root should have units of $m/s$ (because it’s mean speed). The exponent is unitless, $N_A$ has units of $1/mol$, and product of concentrations has units $mo{l}^2/L^2$. Overall, the product is $m^3/s\times mol/L^2$. We can recognize that $1m^3=1000L$, then the units reduce to $mol/(L\ast s)$ which is exactly the rate of change of concentration!

Let’s rewrite the rate in these units

$$r=\sigma \sqrt{\frac{8RT}{\pi \mu }}10^9{N}_A{e}^{-E_a/RT}[A][B]$$

now, if we define $A=\sigma \sqrt{\frac{8RT}{\pi \mu }}10^9{N}_A$, and $k=A{e}^{-E_a/RT}$, we recover the the rate law!

Steric Factor

We might calculate predictions of $A_{\text{theory}}$ values, and then compare those to experimental values and find that we might have some discrepancy. Oh no, what should we do? In situations like this, scientists like to introduce proportionality constants which fix everything. What’s missing from our model? Well, we have a key assumption, that all collisions with enough energy turn into reactions. But we never said anything about orientations right, and intuitively, the molecules should collide with proper orientation. So ideally, $A_{\text{experiment}}/A_{\text{theory}}$ should be less than 1. We define this ration to be the steric factor $P$. So we fix our rate law by adding this extra parameter:

$$r=P\sigma \sqrt{\frac{8RT}{\pi \mu }}10^9{N}_A{e}^{-E_a/RT}[A][B]$$

Let’s see some examples:

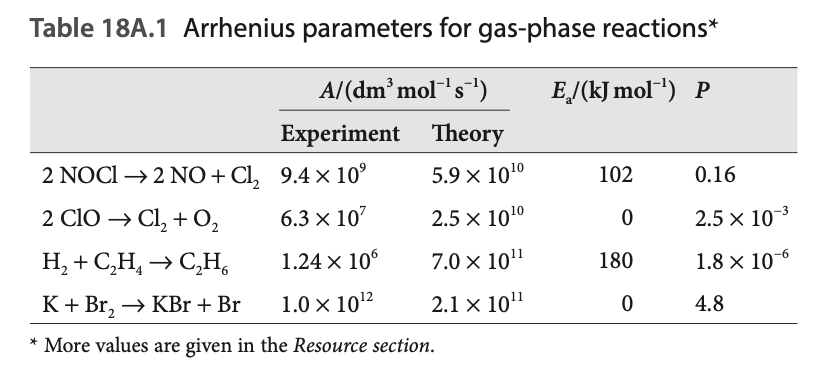
Oh no, $P>1$. What do we do? Pretend it’s all good :) In seriousness, if we consider $P$ as just the metric of proper orientation, I find it hard to justify values $P>1$, but if we consider $P$ as a collection of everything missing from our fairly simple model, then sure, why not.