Review for Exam 1

The purpose of this note is to briefly re-iterate key concepts from the past few weeks in preparation for exam 1 through a cohesive story, which, I hope, will help you to prepare more and have more confidence.

A few meta notes. First, please review Problem-Solving Strategies. Second, make sure you understand all the concepts we’ve covered. I haven’t seen the exam, but looking at practice exam and thinking from first principles, my best guess is that the exam may focus on understanding subtle differences such as the difference between “reaction rate” and “rate of consumption/production” or the difference between “Q” and “K”. Thus, if you don’t feel like you fully understand a concept, do something until you understand it (you can email me [email protected], use perplexity.ai, chat.openai.com, claude.ai or Google Bard).

Now, let’s begin the review.

Reaction Rate

We began by reflecting on our intuitive notions of how fast chemical reactions occur and ended up agreeing, that what matters is how fast the concentration changes. Let’s consider the following chemical reaction:

$$a\mathrm{A}+b\mathrm{B}\to c\mathrm{C}+d\mathrm{D}\text{\hspace{1em}(1)}$$

At first, we calculate average speed of production of $C$.

$$\frac{\Delta [C]}{\Delta t}=\frac{[C{]}_{t=2}-[C{]}_{t=1}}{t_2-t_1}\text{\hspace{1em}(2)}$$

But then we recognize that the rates of production of $C$ and of $D$ may be different (if $c\ne d$). However, we don’t see any benefit in 4 different reaction rates (or even more, if you have more molecules), so we recognize that if we divide the rates of production/consumption by stoichiometric coefficients, we should get the same values of rates. In other words, equation (3) is satisfied:

$$-\frac{1}{a}\frac{\Delta [A]}{\Delta t}=-\frac{1}{b}\frac{\Delta [B]}{\Delta t}=\frac{1}{c}\frac{\Delta [C]}{\Delta t}=\frac{1}{d}\frac{\Delta [D]}{\Delta t}\text{\hspace{1em}(3)}$$

Then we recognize that reaction with different intuitive rates may have the same average speed, which makes us recognize the importance of instantaneous speed which is defined to be the limit of (2) when $\Delta t\to 0$:

$$\underset{\Delta t\to 0}{\lim }\frac{\Delta [C]}{\Delta t}=\frac{d[C]}{dt}\text{\hspace{1em}(4)}$$

We can rewrite (3) in terms of instantaneous speeds as well, this time introducing the symbol $r$ for instantaneous reaction rate.

$$-\frac{1}{a}\frac{d[A]}{dt}=-\frac{1}{b}\frac{d[B]}{dt}=\frac{1}{c}\frac{d[C]}{dt}=\frac{1}{d}\frac{d[D]}{dt}=r\text{\hspace{1em}(5)}$$

What kind of problems can you expect for this concept? You may be given reaction rates (i.e. $\frac{1}{c}\frac{d[C]}{dt}$) and asked to calculate rates of consumption/production (i.e. $\frac{dA}{dt}$, $\frac{d[C]}{dt}$) or vice versa. Key to success is rewriting the data given in the problem in symbolic form, so that you leave no room for confusion whether the value you have is already multiplied by factors like $1/c$ or not. After that, it’s straightforward application of (5).

Then we may wonder, well, how do we compute that instantaneous speed? We are told (but you can also see the derivation, if you don’t like to take things for granted) that there is a theory called Collision Theory, which proposes that the instantaneous reaction rate is given by (6):

$$r=k[A{]}^m[B{]}^n\text{\hspace{1em}(6)}$$

where $k$ is some constant of proportionality, which we call the rate constant, $m,n$ are some (not necessarily integer) numbers, which we call reaction order with respect to A and B respectively. These $m$ and $n$ are equal to $a$ and $b$ only for elementary reactions, i.e. reactions for which equations correspond to the mechanism. Quite often these are unimolecular or bimolecular reactions, and rarely trimolecular.

a typical problem testing these concepts would have asking you to determine $m,n$ based on instantaneous reaction rates at different concentrations. If there are no two rows with the same concentrations for all but one reactant, please do not panic and simply approach it systematically: write $r_1$ (for some row 1) as $r_1=k[A{]}_1^m[B{]}_1^n$. Then write $r_2=k[A{]}_2^m[B{]}_2^n$. If you know one of $m,n$, you have two equations with two unknowns: $k$ and whichever of $m,n$ you didn’t know. If you didn’t know both $m,n$, write the same thing for row 3, so now you have 3 equations. From that moment, it’s algebra.

We may also have more complex reactions like:

$$2\mathrm{NO}+\mathrm{H}{}_2\to \mathrm{N}{}_2\mathrm{O}+\mathrm{H}{}_2\mathrm{O}\text{\hspace{1em}(7)}$$

which consists of two steps:

$$\begin{array}{rl}2\mathrm{NO}& \underset{\mathrm{k}{}_{-1}}{\overset{\mathrm{k}{}_1}{\rightleftharpoons }}\mathrm{N}{}_2\mathrm{O}{}_2\\ \mathrm{N}{}_2\mathrm{O}{}_2+\mathrm{H}{}_2& \stackrel{\mathrm{k}{}_2}{\to }\mathrm{N}{}_2\mathrm{O}+\mathrm{H}{}_2\mathrm{O}\end{array}\text{\hspace{1em}(7.1)(7.2)}$$

for which we can separately write reaction rates using the rate law:

$$r_{7.1-fwd}=k_1[\mathrm{NO}{]}^2{r}_{7.1-rvr}=k_{-1}[\mathrm{N}{}_2\mathrm{O}{}_2]r_{7.2}=k_2[\mathrm{N}{}_2\mathrm{O}{}_2][\mathrm{H}{}_2]\text{\hspace{1em}(8)}$$

Can we write the overall reaction rate? Yes, but it’s better to come back to it once we review concepts of equilibrium.

Reaction Diagrams

After looking at reaction rates, we’re introduced to the energy diagram of reactions. The general idea is this: we have some energy scale. There’s a position for a reactant and a product. For exothermic reactions, products are lower in energy than reactants. For endothermic reactions, products are higher in energy than reactants. Then we claim that the only way to connect reactants to products is through a curve which looks like a hill, i.e. has a peak that is not a reactant or a product. We call that state with highest energy the transition state.

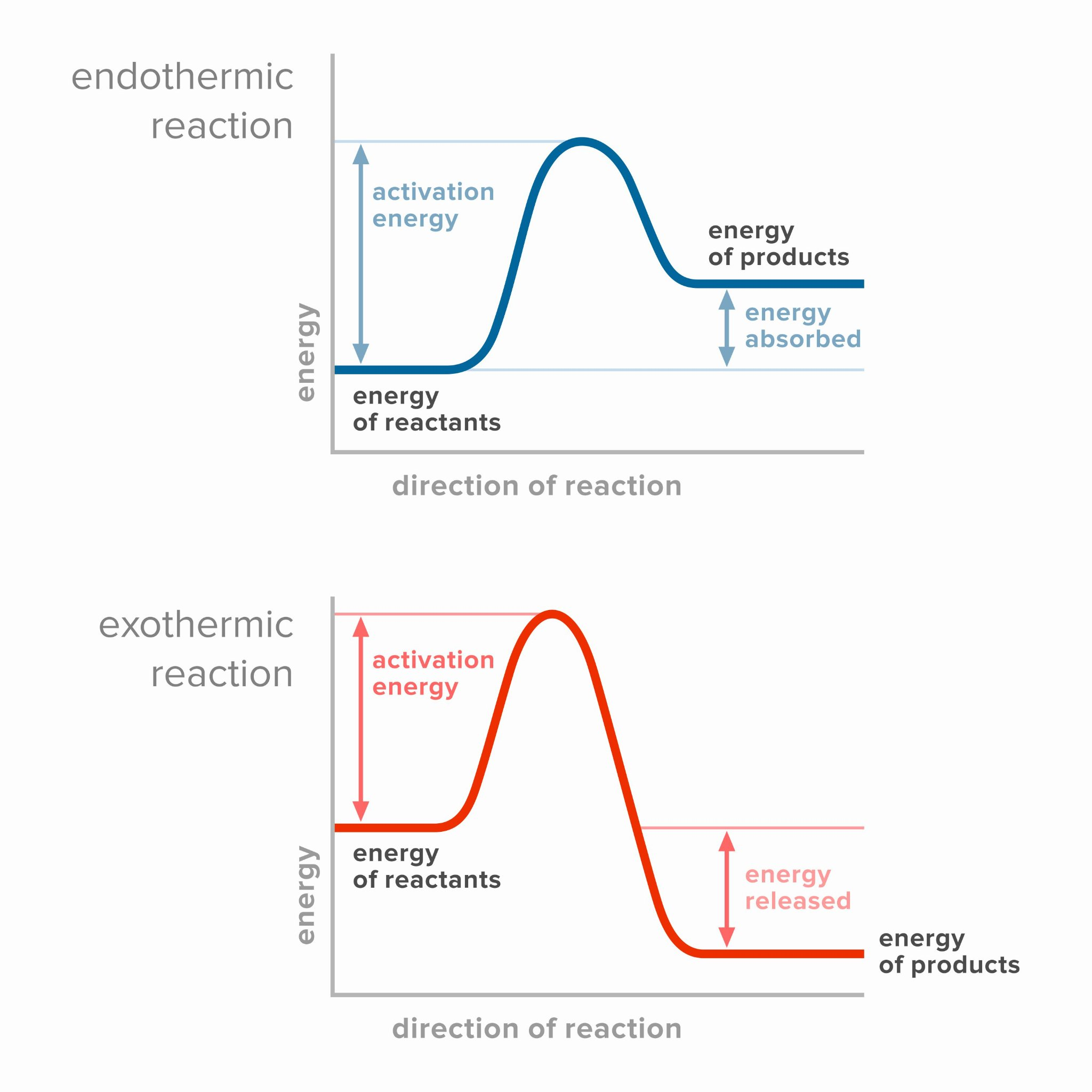
If you read my notes on Transition State, you know that this shape of the reaction curve follows from the shape of the potential energy for a chemical bond.

Equilibrium

As soon as we learn the shape of the reaction curve and are told that before reactants convert to products, they have to surpass (or, to be more precise, have total energy, kinetic + potential, greater than the energy of the barrier) the energy barrier, we might ask: what stops molecules from moving in the other direction, from products to reactants?

In most cases, nothing. So in addition to equation (1), we can write equation (9):

$$c\mathrm{C}+d\mathrm{D}\to a\mathrm{A}+b\mathrm{B}\text{\hspace{1em}(9)}$$

What could prevent this reaction from happening? Lack of collisions between C and D. Why would we not have those collisions? If C and/or D are not present in the solution! One or both may precipitate, or leave the liquid as gas, or maybe form some very strong complex with some other molecule.

Because it is a bit inconvenient to write two equations (1) and (9) for essentially the same system, we introduce the double-headed arrow $\rightleftharpoons$:

$$a\mathrm{A}+b\mathrm{B}\rightleftharpoons c\mathrm{C}+d\mathrm{D}\text{\hspace{1em}(10)}$$

Equation (10) is equivalent to (1) and (9) in combination. You can always write any reversible reaction as two separate equations, one for the forward and one for the reverse direction.

We then ask if there is any special state of a reversible system. I claim that one special moment is when concentrations stop changing over time. In the same note, I show how that concept, translated into math, results in the equality between the rates of forward and reverse reactions:

$$r_{\text{fwd}}=r_{\text{rvr}}\text{or}{k}_1[A{]}_{\text{eq}}^a[B{]}_{\text{eq}}^b=k_{-1}[C{]}_{\text{eq}}^c[D{]}_{\text{eq}}^d\text{\hspace{1em}(11)}$$

when (11) is satisfied, the forward and reverse reactions still happen, $A$‘s collide with $B$‘s to form $C$‘s and $D$‘s, but the amount of $C$‘s and $D$‘s formed is equal to the amount of $C$‘s and $D$‘s that collide and form $A$‘s and $B$‘s. As a result, we have an impression that concentrations do not change over time. We call such state a dynamic equilibrium.

We notice that we can rearrange (11) to:

$$\frac{[C{]}_{\text{eq}}^c[D{]}_{\text{eq}}^d}{[A{]}_{\text{eq}}^a[B{]}_{\text{eq}}^b}=\frac{k_1}{k_{-1}}\text{\hspace{1em}(12)}$$

and the right hand side is clearly a constant for any given reaction. We decide to give it a special symbol $K$ and a name of the equilibrium constant:

$$K\equiv \frac{k_1}{k_{-1}}\text{\hspace{1em}(13)}$$

But (12) also implies that:

$$K=\frac{[C{]}_{\text{eq}}^c[D{]}_{\text{eq}}^d}{[A{]}_{\text{eq}}^a[B{]}_{\text{eq}}^b}\text{\hspace{1em}(13)}$$

we have to be careful and remember that only the ratio of equilibrium concentrations is equal to the equilibrium constant. We decide to call any general ratio of concentrations $Q$:

$$Q=\frac{[C{]}^c[D{]}^d}{[A{]}^a[B{]}^b}\text{\hspace{1em}(14)}$$

And remind ourselves that $Q=K$ only when every concentration is the equilibrium concentration. As a result, we may compute $Q$ and use it as a mathematical test of whether our system is at equilibrium. If $Q>K$, it means we have relatively more products than we should have at equilibrium, so we can predict that the reverse reaction will be faster (its rate is proportional to the concentrations of products) and the amount of products will decrease until the system reaches the equilibrium.

Reactions in Gas Phase

Whenever we deal with reactions in gas phase, we rarely speak of concentrations of gases. More often we describe the relative quantity of a gas by it’s pressure. Luckily, we can express concentration through pressure, if we assume all our particles behave as ideal gas:

$$pV=nRT⟹p=\frac{n}{V}RT=C_{M}RT\text{\hspace{1em}(15)}$$

where $C_M$ is the molar concentration. As a result:

$$[A]=\frac{p_A}{RT}\text{\hspace{1em}(16)}$$

Substituting these into (13) will leave us with:

$$K_C=\frac{[C{]}_{\text{eq}}^c[D{]}_{\text{eq}}^d}{[A{]}_{\text{eq}}^a[B{]}_{\text{eq}}^b}=\frac{(p_C{)}_{\text{eq}}^c(p_D{)}_{\text{eq}}^d}{(p_A{)}_{\text{eq}}^a(p_B{)}_{\text{eq}}^b}{\left(\frac{1}{RT}\right)}^{c+d-a-b}\text{\hspace{1em}(17)}$$

we define the first fraction to be $K_P$ and then denote $c+d-a-b=\Delta n$. As a result:

$$K_c=K_p(RT{)}^{-\Delta n}⟺K_p=K_c(RT{)}^{\Delta n}\text{\hspace{1em}(18)}$$

Which allows us to convert between $K_p$ and $K_c$.

Going back to mechanisms

Recall that we looked at reaction (7)

$$2\mathrm{NO}+\mathrm{H}{}_2\to \mathrm{N}{}_2\mathrm{O}+\mathrm{H}{}_2\mathrm{O}\text{\hspace{1em}(7)}$$

which consisted of two steps:

$$\begin{array}{rl}2\mathrm{NO}& \underset{\mathrm{k}{}_{-1}}{\overset{\mathrm{k}{}_1}{\rightleftharpoons }}\mathrm{N}{}_2\mathrm{O}{}_2\\ \mathrm{N}{}_2\mathrm{O}{}_2+\mathrm{H}{}_2& \stackrel{\mathrm{k}{}_2}{\to }\mathrm{N}{}_2\mathrm{O}+\mathrm{H}{}_2\mathrm{O}\end{array}\text{\hspace{1em}(7.1)(7.2)}$$

for which we could separately write reaction rates using the rate law:

$$r_{7.1-fwd}=k_1[\mathrm{NO}{]}^2{r}_{7.1-rvr}=k_{-1}[\mathrm{N}{}_2\mathrm{O}{}_2]r_{7.2}=k_2[\mathrm{N}{}_2\mathrm{O}{}_2][\mathrm{H}{}_2]\text{\hspace{1em}(8)}$$

Now we’re well equipped to answer the question of what is the overall rate. The overall reaction rate is equal to the rate of the slowest step (we, therefore, call it rate-determining). Why? Look back at the energy diagram for a chemical reaction: for a reaction to occur, the molecule should have more total energy than the highest peak. If a molecule can pass a high peak, it can easily pass any other peak of lower height. Therefore, we have to identify the rate-determining step (RDS). We can safely ignore all steps that succeed the RDS because of the peak argument above. We’ll have to consider the steps that precede RDS (if such exist) because the rate of the RDS will depend on concentration of products of those steps, and we want to only have dependence on the reactants of the overall reaction.

Consider our system above. If (7.1) is RDS, then the reaction rate is equal to the rate of the 7.1:

$$r=r_{7.1}=k_1[NO{]}^2\text{\hspace{1em}(19)}$$

We’re done.

If (7.2) is RDS, then we have to assume that the step (7.1) is fast enough for the equilibrium to be established. It’s possible to find overall reaction rate (as I did here) without that assumption, but in this class you are not expected to be able to do that. So, if (7.1) is fast enough for the equilibrium to be established, then, by (11)

$$k_1[\mathrm{NO}{]}^2=k_{-1}[\mathrm{N}{}_2\mathrm{O}{}_2]\text{\hspace{1em}(20)}$$

and we know that the overall rate is equal to the rate of 7.2 (because it’s the RDS):

$$r=k_2[\mathrm{N}{}_2\mathrm{O}{}_2][\mathrm{H}{}_2]\text{\hspace{1em}(21)}$$

This rate depends on the concentration of an intermediary product $\mathrm{N}{}_2\mathrm{O}{}_2$, but we can easily get rid of it using (20):

$$r=\frac{k_1{k}_2}{k_{-1}}[\mathrm{NO}{]}^2[\mathrm{H}{}_2]\text{\hspace{1em}(22)}$$

where we can define $\frac{k_1{k}_2}{k_{-1}}$ to be effective or overall rate constant $k$.

The Secret To Passing Any Exam

I understand that many of you may have an urge to stay very late and prepare for the exam. The single best piece of advice I could give to you is do not stay later than 10-11pm. Your brain needs q u a l i t y sleep to function properly and no subject or an exam is worthy of sacrificing that q u a l i t y sleep. Also, I guess you already know that any exam or a test is nothing more than a measure of some combination of how much you know and how well you perform under time constraints. It’s not a measure of your personal worthiness or anything like that. Which is also related to an unspoken rule of happy & productive life — you should never tie your sense of self-worth to any external metric.

Misc

Here’ll be answers to some questions I received over email which benefit from me being able to write formulas.

Q7 from practice

$$\begin{array}{rl}\mathrm{NO}+\frac{1}{2}\mathrm{O}{}_2& \stackrel{\mathrm{K}{}_1}{\rightleftharpoons }\mathrm{NO}{}_2\\ \frac{1}{2}\mathrm{N}{}_2+\frac{1}{2}\mathrm{O}{}_2& \stackrel{\mathrm{K}{}_2}{\rightleftharpoons }\mathrm{NO}\end{array}$$

The question is why do we multiply $K_1$ by $K_2$ if we want to find the equilibrium constant of the sum of these two reactions? Let’s find the sum of these two reactions:

$$\frac{1}{2}\mathrm{N}{}_2+\mathrm{O}{}_2\stackrel{\mathrm{K}}{\rightleftharpoons }\mathrm{NO}{}_2$$

Let’s write the equilibrium constant:

$$K=\frac{[\mathrm{NO}{}_2]}{[\mathrm{N}{}_2{]}^{1/2}[\mathrm{O}{}_2]}$$

Let’s also write out the equilibrium constants for individual reactions:

$$K_1=\frac{[\mathrm{NO}{}_2]}{[\mathrm{NO}][\mathrm{O}{}_2{]}^{1/2}}{K}_2=\frac{[\mathrm{NO}]}{[\mathrm{N}{}_2{]}^{1/2}[\mathrm{O}{}_2{]}^{1/2}}$$

What happens if we multiply $K_1$ by $K_2$?

$$K_1\times K_2=\frac{[\mathrm{NO}{}_2]}{[\mathrm{NO}][\mathrm{O}{}_2{]}^{1/2}}\times \frac{[\mathrm{NO}]}{[\mathrm{N}{}_2{]}^{1/2}[\mathrm{O}{}_2{]}^{1/2}}=\frac{[\mathrm{NO}{}_2]}{[\mathrm{N}{}_2{]}^{1/2}[\mathrm{O}{}_2]}$$

we get $K$!

Is this an accident? No, it’s a more general result that can be proven mathematically once we’ll learn about the connection between $K$ and some thermodynamic quantity.