Empirical Observations for Rate Laws (Lecture 3)

Just a few almost random notes for some slides in Lecture 3.

Second-order reactions are slower than zero-order?

Look at slide 12

That’s true … sometimes. Recall that the rate law for an $n$-th order reaction is:

$$r=k[A{]}^n$$

Let’s fix $k=1$, call $y=r$ and $[A]=x$. Essentially, this boils down to comparing functions of the form $y=1$, $y=x$, $y=x^2$. Let’s use Desmos and plot these functions:

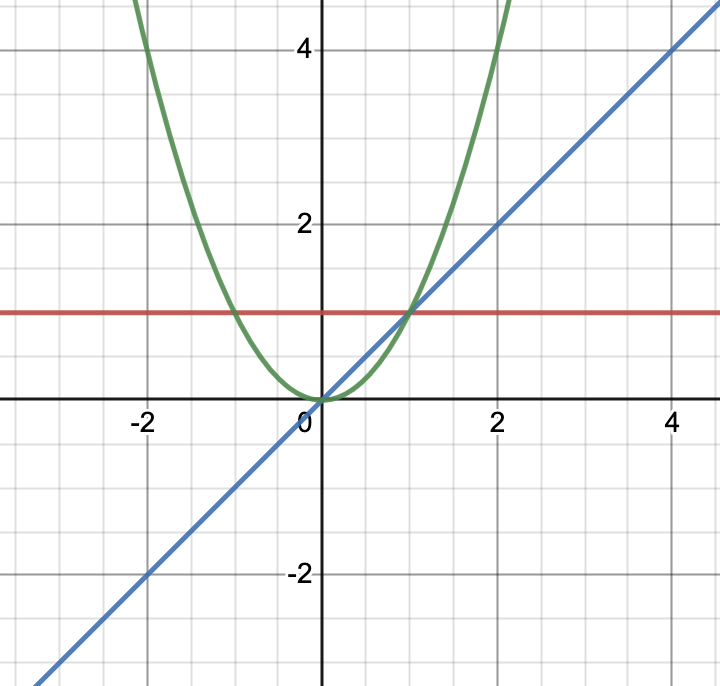
Wait a second, but $y=x^2$ (green curve) is way above $y=x$ blue curve, so why is second-order reaction slower than first-order? Let’s focus on the region $x\in [0,1]$:

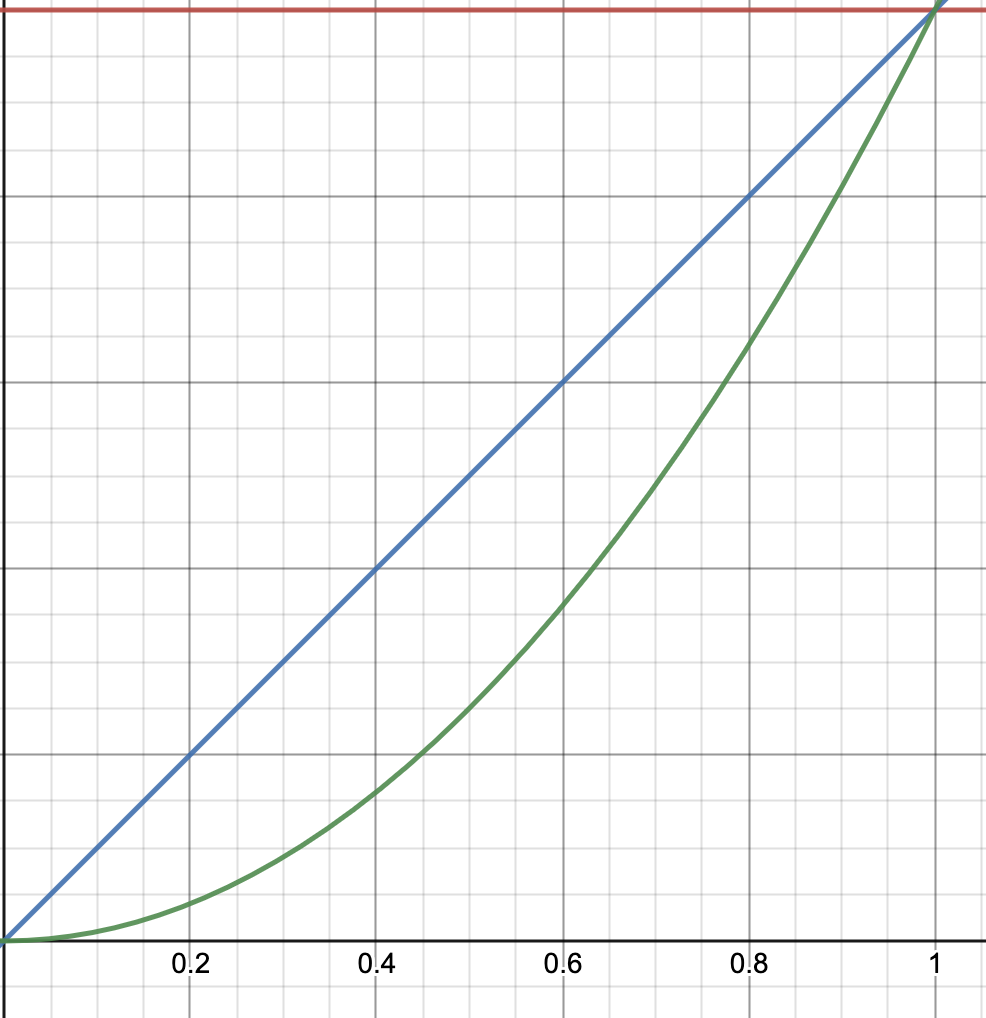
a more familiar picture! or at least, the one, which corresponds to the one on the slide. In practice, we often use concentrations smaller than 1, (if you pay attention, most problems involve concentrations with orders $10^{-1}$ down to $10^{-6}$, if not smaller). Therefore, the more times we multiply $k$ by $[A]$, the smaller the final number will be.

This also explains slide 11. If second-order reaction is slower (under $[A]<1$), then the $[A]$ will decrease more slowly.

Units for Rate Constant

A way to avoid memorizing table from slide 20 is to recall the definition of the reaction rate:

$$r=\frac{\Delta [A]}{\Delta t}$$

The numerator is in M or mol/L (or $\mathrm{mol}\cdot \mathrm{d}{\mathrm{m}}^{-3}$ if you insist), the denominator is in s. Therefore, the units of the rate are: $\mathrm{mol}{\mathrm{L}}^{-1}{\mathrm{s}}^{-1}$. These are the units of $r$, regardless of the form of the reaction rate law or specific orders. Thus, one can figure out the units of the rate constant by working from the units of the reaction rate:

$$r=k[A{]}^m[B{]}^n$$

knowing particular values of $m$ and $n$, your task is to figure out what you should multiply by $\mathrm{mol}{\mathrm{L}}^{-1}$ or M $m+n$ times so that you get $\mathrm{mol}{\mathrm{L}}^{-1}{\mathrm{s}}^{-1}$ or $\mathrm{M}{\mathrm{s}}^{-1}$.

I finished writing this JUST when Dr. Cooper started telling the same thing… Sometimes it’s beneficial to wait. sometimes

Questions from the Audience

What’s up with Orders

It seems to bother people that the reaction orders do not correspond to the stoichiometric coefficients, so let me give you some info in case you can’t wait until we actually cover it.

Turns out, there are two types of chemical equations: the ones, which correspond to mechanisms, and the ones which only summarize the mechanism.

In other words, when we write $\mathrm{A}+\mathrm{B}\to \mathrm{C}$, this rarely corresponds to molecule $A$ colliding with $B$ and forming $C$. It may, but I can’t even think of an example when it actually does. Consider $\mathrm{H}{}_2+\mathrm{I}{}_2=2\mathrm{HI}$. You might be tempted to think $\mathrm{H}{}_2$ collides with $\mathrm{I}{}_2$ and forms $\mathrm{HI}$, but actually the reaction happens in three steps:

$$\begin{array}{rl}& \mathrm{I}{}_2\stackrel{\mathrm{k}{}_1}{\to }2\mathrm{I}\\ & \mathrm{I}+\mathrm{H}{}_2\stackrel{\mathrm{k}{}_2}{\to }\mathrm{HI}+\mathrm{H}\\ & \mathrm{H}+\mathrm{I}{}_2\stackrel{\mathrm{k}{}_3}{\to }\mathrm{HI}+\mathrm{I}\\ & \mathrm{H}+\mathrm{I}\stackrel{\mathrm{k}{}_4}{\to }\mathrm{HI}\\ & \mathrm{H}+\mathrm{H}\stackrel{\mathrm{k}{}_5}{\to }\mathrm{H}{}_2\\ & \mathrm{I}+\mathrm{I}\stackrel{\mathrm{k}{}_6}{\to }\mathrm{I}{}_2\end{array}$$

The first reaction is what’s known as initiation, the second and third propagation, and the rest are termination reactions

they are named by the number of radicals formed, if you know what radicals are. If 2 radicals form from a neutral compound it’s an initiation, if a radical reacts with a neutral molecule and forms another neutral molecule with another radical it’s a propagation, finally when two radicals collide to form a neutral molecule, it’s a termination

What’s important here, is that the familiar rate laws can be written for each of those individual reactions, and the orders will correspond to stoichiometric coefficients, because these reactions are primary or elementary reactions. In other words, the reaction rate of termination 6 is:

$$r_6=k_6[I{]}^2$$

If we’re interested in the overall reaction rate (for simplicity, let’s focus on the rate of production of $\mathrm{HI}$), we might notice that $\mathrm{HI}$ forms through three different channels $2,3,4$, so we have to sum different reaction rates. But then some compounds are consumed in other reactions, so overall, once we do some algebra, we’ll end up with some complicated reaction rate, which MAY look like:

$$r=k[H_2][I_2]$$

But may as well look like

$$r=\frac{k[H_2][I_2]}{k_7[H_2]+k_8[I_2]}$$

and so what is the order? Well, if $k_7$ is incredibly big, $k_7\gg k_8$ such that $k_7[H_2]\gg k_8[I_2]$, we have:

$$r=\frac{k[H_2][I_2]}{k_7[H_2]+k_8[I_2]}\approx \frac{k[H_2][I_2]}{k_7[H_2]}=\frac{k}{k_7}[I_2]$$

that’s how we may have a zero-th order even though $H_2$ participates in the reaction! If we take another limit, when $k_7$ is big time small, $k_7[H_2]\ll k_8[I_2]$, we’ll end up with $r\approx k/k_8[H_2]$. So we see that depending on the values of rate constants the order of $[H_2]$ (and $[I_2]$ for that matter) will vary from $0$ to $1$. That’s how we may empirically observe non-integer values of rate orders.

Initial Rates are similar?

Q: if we look back at the graph, we see that reaction rates are very similar at the beginning, so how we might distinguish between different orders?

Dr. Cooper mentioned that the graph is only for a single reactant reaction, but I think it may not answer the question. What’s important is that to find out the rate, we compare the reaction rates at different initial concentrations of $[A]$.

In other words, in practice, let’s say we look at $\mathrm{A}\to \mathrm{P}$. We prepare the solution with $[A]=0.01M$, somehow initiate the reaction and measure instantaneous rate $r_1$. Then we repeat the process with $[A]=0.02M$ and measure the rate $r_2$. Then:

$$r_1=k[A{]}_1^n{r}_2=k[A{]}_2^n⟹\frac{r_2}{r_1}={\left(\frac{[A{]}_2}{[A{]}_1}\right)}^n$$

We might continue by taking logarithm of both sides

$$\begin{array}{rlrl}\ln \frac{r_2}{r_1}& =\ln {\left(\frac{[A{]}_2}{[A{]}_1}\right)}^n& & \\ \ln \frac{r_2}{r_1}& =n\ln \left(\frac{[A{]}_2}{[A{]}_1}\right)& & \text{properties of logarithm}\\ \frac{\ln \frac{r_2}{r_1}}{\ln \frac{[A{]}_2}{[A{]}_1}}& =n& & \end{array}$$

which gives a convenient formula for determining the order of a reaction. It works for any reaction as long as only one reagent’s concentration is changed.