Reaction Speed (Lecture 1)

What is the difference between a slow and a fast reactio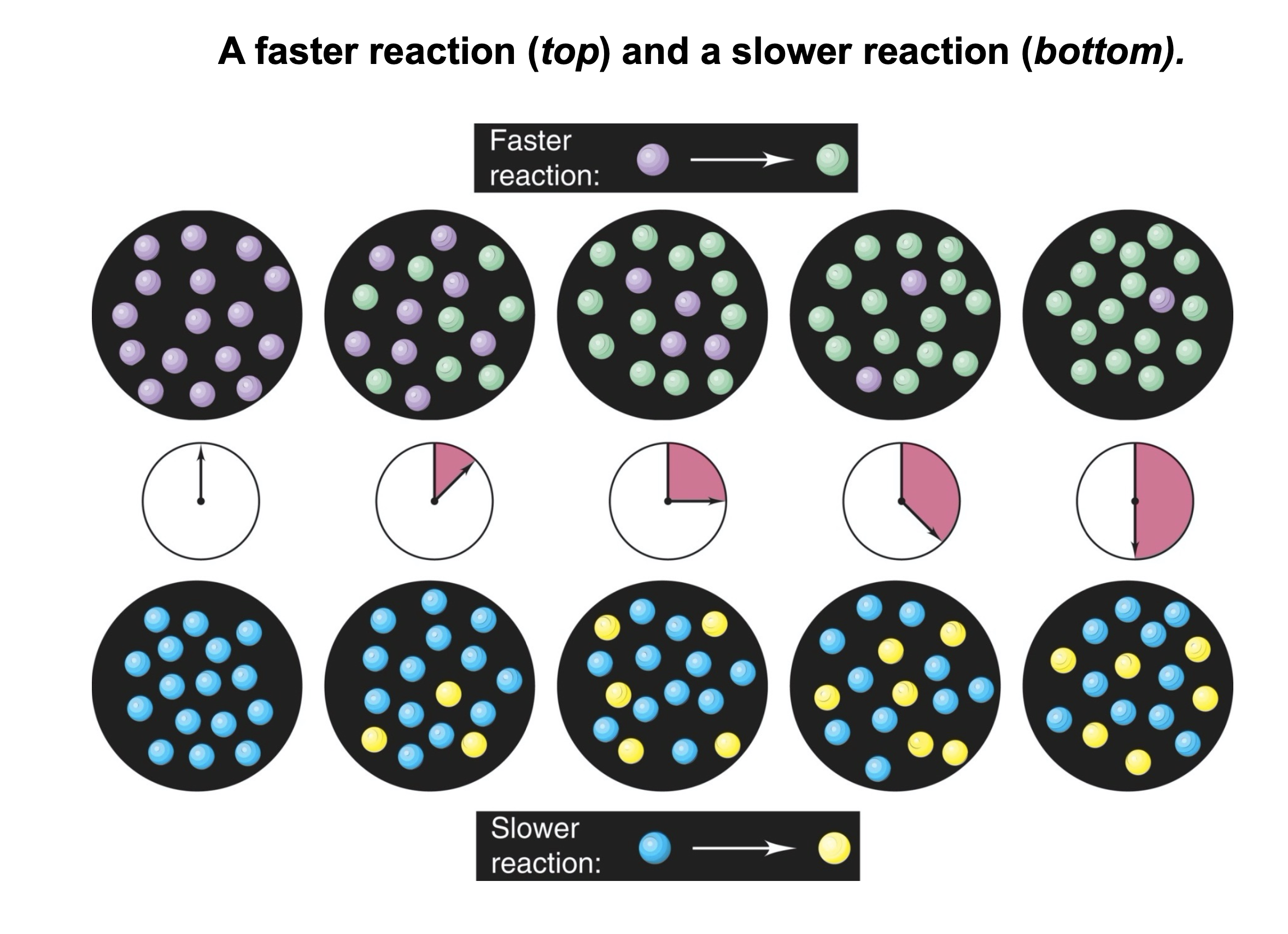n? Looking at Slide 1 Q: which reaction is faster? A: the one which is labeled faster reaction…

Intuitively, even without the label we may identify the top reaction as being faster. Why might we conclude that? It is tempting to say it has a higher rate, but it is important to separate inferences from the facts presented.

In the picture, we do not see a “reaction rate”. Instead, what we see is the number of particles of color A and the number of particles of color B at different timesteps. Let’s say the products have color B. We might say that if we start from the all particles colored A and then in one reaction after some amount of time there are more particles B than in another reaction, we might call this a faster reaction. In other words, we intuitively associate rate with the speed at which the number of particles changes.

If we think about it for a while, we might notice that for every new color B particle, there is one fewer color A particle. In other words, we might infer the rate judging both by appearance of B and by disappearance of A. This is a key insight, that we shall come back to later.

At this point, let’s remember that we intuitively define a rate of the chemical reaction $A\to B$ as the increase in the number of particles of B (or decrease in the number of particles of A) in a given amount of time.

Factors influencing reaction rate

Which factors influence the speed of a chemical reaction? A meta discussion was moved here: Finding Factors Affecting X

In this case, we’re interested in chemical reactions, so that’s our system. Our output variable of interest is how fast it happens (the rate). Quite often we figure out all the inputs by first describing the mechanism (because then all the inputs become evident).

What is a chemical reaction?

Fundamentally, a chemical reaction occurs when two particles which have enough energy collide in a proper orientation. Can more than two particles collide? Yes, trimolecular reactions exist, but they’re quite rare and for now, let’s focus on bimolecular reactions. Okay, that’s our mechanism; what are the inputs? The inputs are:

1. occurrence of a collision (or, quantitatively, the frequency of collisions)
2. particles having enough energy

Frequency of Collisions

Let’s dissect each one separately. What affects the number of collisions that happen in a unit of time (which is frequency, by definition)? Well, to answer that question, we must first understand how particles move. At first, we focus on particles in gas state. One reason - they are simpler, a more satisfactory reason - systems in liquid phase share the same fundamentals and differ in some peculiarities which complicate some aspects.

So how do particles move? Each particle moves in a straight line with a given velocity (which is vector, i.e. has magnitude and direction) until it hits either a wall or other particle. The collision with the wall effectively inverses one of the components of the velocity vector (magnitude unchanged), and the collision with other particles in the simple case is treated as an elastic collision (i.e. no energy loss). The point being, two particles (1 and 2) with masses $m_1$ and $m_2$ and velocities ${\vec{v}}_1^{(i)}$ and ${\vec{v}}_2^{(i)}$ collide and post collision move with some new velocities ${\vec{v}}_1^{(f)}$ and ${\vec{v}}_2^{(f)}$.

Okay, so how do we increase the frequency of collisions? If you think about it, there are two ways: increase the chance of a collision from the first attempt and (or) increase the number of attempts. To increase the former, i.e. increase the chance that a particle will meet another particle on its route, we can:

1. realize that the chances are higher if there are more particles to collide with. If we think a bit more carefully, we’ll realize that we have to count the relative number of particles per some unit of area or volume (it matters a lot whether there are 100 particles spread over a football stadium or a tiny matchbox). That relative number is concentration, by definition.
2. realize that the chances are higher if the particles are larger (and so it’s hard to not stumble upon them). And, in fact, the reaction rate does depend on the radii of two particles although this is rarely mentioned.

How might we increase the number of attempts the particle have at collision? We can make them move faster (increase their speed). Temperature is a convenient statistical description of a distribution of speeds of particles, so quite often whenever we say we want to increase particle speeds, we simply say we will increase temperature.

Energetics of reaction

Chemical reaction is always accompanied by the destruction of some chemical bonds (and creation of others). Even though you may be better off in the end ($\Delta G<0$, in case you’re familiar with the concept of Gibbs energy), at first you have to pay the cost (destruction of a chemical bond requires energy). You may have seen the following diagram:

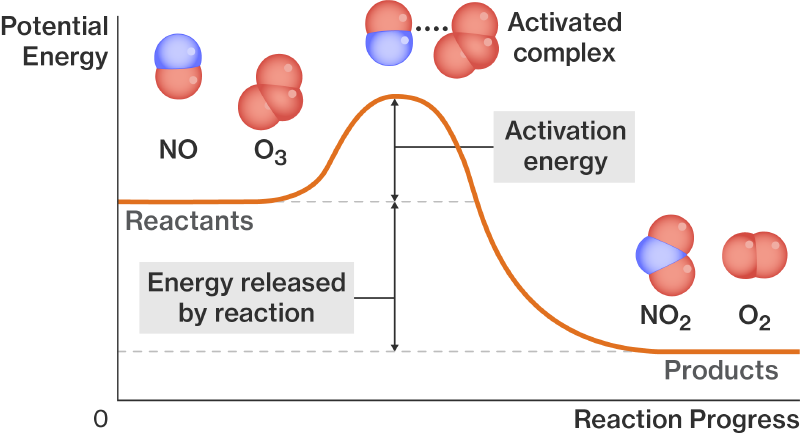
this diagram is a bit misleading as many people infer that reactants have to climb over some hill of energy barrier before they can react and form products. In reality, what this diagram shows is the “internal” energy of reactants, transition states, and products. The energy that comes from having certain chemical bonds, having attractions between different nuclei and electrons, and repulsions among nuclei and repulsions among electrons. What we should also consider is the thermal energy (or kinetic energy) of particles. Sometimes it is included in such diagrams (when we say that a diagram is drawn for a certain temperature), but the problem is, at any given $T$ we never have all particles moving with the same speed. There’s always a distribution of speeds (Maxwell-Boltzmann, if you’ve heard of that), and so there’s always a distribution of kinetic energies. So instead of having a single starting position for reactants, we should have a distribution. And it turns out, energies of some reactants (when kinetic contribution is included) are above the activation energy barrier. In fact, the $e^{E_a/RT}$ factor in the Arrhenius law (in case you’ve seen it) is exactly the share of particles which have an energy above the activation energy $E_a$.

To reiterate, reactions occur when particles collide and when they have enough energy. They should have enough energy even before the collision. That energy comes from the structure of particles (so it’s something fixed for any given reaction) and from their kinetic energy (which is directly linked to speeds, which are described by temperature). So, if we want to increase the fraction of molecules that have enough energy to react, we need to increase temperature.

Let’s sum all the factors we described above:

1. Concentration: the more there are particles, the larger the chance that any moving particle will collide with some other particle (we increase the number of attempts at collision)
2. Sizes of particles: the larger the particle is, the larger the chance that two moving particles will meet each other (we increase the chance of collision from the first attempt)
3. Speeds of particles: the faster particles move, the more attempts at collision they have. Particles move faster when they have higher temperature.
4. Also, faster particles have greater kinetic energy, and so it’s more likely that their total energy is above the energy barrier $E_a$.

Which is essentially what’s written on Slide 2. The role of a catalyst is to simply change the mechanism of the reaction (and so change $E_a$ and for it to be a catalyst, the $E_a$ should decrease).

There was a question about the pressure — pressure is a metric showing the number of collisions of particles with a wall. So it’s a combination of two factors: concentration and temperature. Can you see why?

Questions from the Audience

If we’re interested in the percent yield, do we look at the rate of the consumption of reactant or production of product?

Well, first of all, the two rates are the same (as we realized at the beginning), but second it is important to realize that yield is calculated by comparing the theoretical amount of mass produced to the practical. Chemical kinetics deals with how fast the theoretical (or any other) amount of mass should be produced; it does not deal with why or how the practical mass will end up being smaller than the theoretical.